TorqueNap LogoTorqueNap Blog
← Techに戻る

LightGBMとはなにか？その基本を学ぶ

2025-08-15
#python#machine-learning
LightGBMの仕組みと高速化要因、前処理・実装手順やチューニング・評価、他手法比較を実務目線で解説

LightGBMとは？

LightGBMは、決定木をベースとする勾配ブースティングモデルです。とても高速・高精度で、大規模データやカテゴリ変数・欠損値も前処理最低限で扱うことができます。
公式ドキュメントでも「高速・省メモリ・GPU対応・分散学習可能」が明記されています。（公式ドキュメント）

なぜLightGBMは早くて省メモリなのか？

  • ヒストグラム学習
    • 連続値をビンにまとめ、ビン店に出分割候補を探すことで計算とメモリを大幅に削減。XGBoostの既定アルゴリズム（pro-sort）より最適化しやすい設計
  • Leaf-wise（best-first）成長
    • もっとも損失を減らせる葉を優先して深く伸ばす = 少ない木でも高精度。ただし、深くなりすぎ勝ちで、num_leavesとmax_depthで過学習に注意。
  • GOSS（Gradient-based One-Side Sampling）& EFB（Exclusive Feature Bundling）
    • GOSS: 勾配が小さいサンプルを間引き、情報量の大きいサンプルを重視して高速化
    • EFB: 同時に立たない疎かな特徴量をまとめて次元圧縮。
  • カテゴリ・欠損を素で扱える
    • カテゴリ変数は最適分割できるので、ワンホットエンコーディングなどの前処理が不要。欠損値も自動的に最適な値（既定でNaN）で補完。

どんなときに使うべきか？

  • テーブルデータ（数値＋カテゴリが混在）
  • 特徴量が多い／疎なデータ
  • 前処理を最小限にして素早くベースラインを作りたい時
  • 回帰・2値/多値分類・ランキング（学習目的を切り替え可

まず動かす：10分ハンズオン（分類）

python
# -*- coding: utf-8 -*-
# pip install lightgbm scikit-learn pandas numpy matplotlib

import os
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import japanize_matplotlib 

from lightgbm import LGBMClassifier, early_stopping, log_evaluation
from sklearn.datasets import load_breast_cancer
from sklearn.model_selection import train_test_split
from sklearn.metrics import (
    roc_auc_score, f1_score, classification_report, confusion_matrix,
    roc_curve, precision_recall_curve, average_precision_score,
    brier_score_loss
)
from sklearn.calibration import calibration_curve

# ========================
# 設定
# ========================
SAVE_FIG = True
OUT_DIR = "lgbm_report"
os.makedirs(OUT_DIR, exist_ok=True)


def savefig(name: str):
    if SAVE_FIG:
        path = os.path.join(OUT_DIR, name)
        plt.savefig(path, bbox_inches="tight")


# ========================
# 日本語ラベル（特徴量 & クラス）
# ========================
FEATURE_JA = {
    "mean radius": "平均半径",
    "mean texture": "平均テクスチャ",
    "mean perimeter": "平均周囲長",
    "mean area": "平均面積",
    "mean smoothness": "平均平滑度",
    "mean compactness": "平均コンパクト性",
    "mean concavity": "平均凹み度",
    "mean concave points": "平均凹点数",
    "mean symmetry": "平均対称性",
    "mean fractal dimension": "平均フラクタル次元",
    "radius error": "半径の誤差",
    "texture error": "テクスチャの誤差",
    "perimeter error": "周囲長の誤差",
    "area error": "面積の誤差",
    "smoothness error": "平滑度の誤差",
    "compactness error": "コンパクト性の誤差",
    "concavity error": "凹み度の誤差",
    "concave points error": "凹点数の誤差",
    "symmetry error": "対称性の誤差",
    "fractal dimension error": "フラクタル次元の誤差",
    "worst radius": "最悪半径",
    "worst texture": "最悪テクスチャ",
    "worst perimeter": "最悪周囲長",
    "worst area": "最悪面積",
    "worst smoothness": "最悪平滑度",
    "worst compactness": "最悪コンパクト性",
    "worst concavity": "最悪凹み度",
    "worst concave points": "最悪凹点数",
    "worst symmetry": "最悪対称性",
    "worst fractal dimension": "最悪フラクタル次元",
}

CLASS_LABELS = {0: "悪性", 1: "良性"}  # sklearn乳がんデータ: 0=malignant(悪性), 1=benign(良性)

# ========================
# 1) データ読み込み
# ========================
X, y = load_breast_cancer(return_X_y=True, as_frame=True)

# ========================
# 2) 学習/評価分割（クラス比維持）
# ========================
X_tr, X_te, y_tr, y_te = train_test_split(
    X, y, test_size=0.2, stratify=y, random_state=42
)

# ========================
# 3) モデル定義（基本形）
# ========================
clf = LGBMClassifier(
    n_estimators=2000,
    learning_rate=0.05,
    num_leaves=63,
    subsample=0.9,
    colsample_bytree=0.9,
    class_weight="balanced",
    random_state=42
)

# ========================
# 4) 学習（早期停止つき）
# ========================
clf.fit(
    X_tr, y_tr,
    eval_set=[(X_te, y_te)],
    eval_metric="auc",
    callbacks=[early_stopping(50), log_evaluation(100)]
)

# ========================
# 5) 推論＆指標
# ========================
proba = clf.predict_proba(X_te)[:, 1]
pred_05 = (proba >= 0.5).astype(int)

auc = roc_auc_score(y_te, proba)
ap  = average_precision_score(y_te, proba)
f1_05 = f1_score(y_te, pred_05)
cm_05 = confusion_matrix(y_te, pred_05, labels=[0,1])  # 0=悪性,1=良性
brier = brier_score_loss(y_te, proba)

# 閾値最適化（F1最大）
ths = np.linspace(0.01, 0.99, 99)
f1s = np.array([f1_score(y_te, (proba >= t).astype(int)) for t in ths])
best_idx = int(np.argmax(f1s))
best_th  = float(ths[best_idx])
f1_best  = float(f1s[best_idx])
pred_best = (proba >= best_th).astype(int)
cm_best = confusion_matrix(y_te, pred_best, labels=[0,1])

# ========================
# 6) 可視化
# ========================
# (a) ROC
fpr, tpr, _ = roc_curve(y_te, proba)
plt.figure(figsize=(5,5))
plt.plot(fpr, tpr, label=f"AUC={auc:.4f}")
plt.plot([0,1], [0,1])
plt.xlabel("偽陽性率 (False Positive Rate)")
plt.ylabel("真陽性率 (True Positive Rate)")
plt.title("ROC 曲線")
plt.legend()
savefig("roc_curve.png")
plt.show()

# (b) Precision-Recall
prec, rec, _ = precision_recall_curve(y_te, proba)
plt.figure(figsize=(5,5))
plt.plot(rec, prec, label=f"AP={ap:.4f}")
plt.xlabel("再現率 (Recall)")
plt.ylabel("適合率 (Precision)")
plt.title("適合率–再現率 曲線")
plt.legend()
savefig("precision_recall_curve.png")
plt.show()

# (c) 較正（reliability）
prob_true, prob_pred = calibration_curve(y_te, proba, n_bins=10, strategy="quantile")
plt.figure(figsize=(5,5))
plt.plot(prob_pred, prob_true, marker="o", label="較正曲線")
plt.plot([0,1], [0,1], label="完全較正")
plt.xlabel("予測確率")
plt.ylabel("実際の陽性率")
plt.title(f"較正曲線（Brier={brier:.4f}）")
plt.legend()
savefig("calibration_curve.png")
plt.show()

# (d) 閾値 vs F1
plt.figure(figsize=(7,3.5))
plt.plot(ths, f1s)
plt.axvline(best_th)
plt.xlabel("閾値")
plt.ylabel("F1")
plt.title(f"F1 と 閾値の関係（最良={best_th:.2f}, F1={f1_best:.4f}）")
savefig("threshold_vs_f1.png")
plt.show()

# (e) 予測確率の分布（クラスごと）
plt.figure(figsize=(7,3.5))
plt.hist(proba[y_te==0], bins=30, alpha=0.6, label=f"クラス0（{CLASS_LABELS[0]}）")
plt.hist(proba[y_te==1], bins=30, alpha=0.6, label=f"クラス1（{CLASS_LABELS[1]}）")
plt.xlabel("予測確率（陽性=悪性の確率）")
plt.ylabel("件数")
plt.title("クラス別の予測確率分布")
plt.legend()
savefig("probability_hist_by_class.png")
plt.show()


# (f) 混同行列（0.5 / best_th）
def plot_cm(cm, title, fname):
    plt.figure(figsize=(4.6,4.2))
    plt.imshow(cm, interpolation="nearest")
    plt.title(title)
    plt.xlabel("予測ラベル")
    plt.ylabel("真のラベル")
    ticklabels = [CLASS_LABELS[0], CLASS_LABELS[1]]
    plt.xticks([0,1], ticklabels)
    plt.yticks([0,1], ticklabels)
    for (i, j), v in np.ndenumerate(cm):
        plt.text(j, i, int(v), ha="center", va="center")
    savefig(fname)
    plt.tight_layout()
    plt.show()


plot_cm(cm_05,  "混同行列（閾値=0.50）", "cm_thr0_50.png")
plot_cm(cm_best, f"混同行列（最良閾値={best_th:.2f}）", "cm_best.png")

# (g) 特徴量重要度（split）— 日本語名で表示
split_imp = pd.Series(clf.feature_importances_, index=X.columns)
split_imp = split_imp.sort_values(ascending=True).tail(15)

# 日本語に変換（欠けがあれば元名のまま）
split_imp.index = [FEATURE_JA.get(c, c) for c in split_imp.index]

plt.figure(figsize=(7,6))
plt.barh(split_imp.index, split_imp.values)
plt.xlabel("分割回数ベースの重要度（split）")
plt.title("特徴量重要度（上位15）")
savefig("feature_importance_split_top15.png")
plt.tight_layout()
plt.show()

# (h) 学習曲線（AUC vs iteration）
evals_result = getattr(clf, "evals_result_", None)
if evals_result:
    val_key = list(evals_result.keys())[0]       # 'valid_0'
    metric_key = list(evals_result[val_key].keys())[0]  # 'auc' など
    vals = evals_result[val_key][metric_key]
    xs = np.arange(1, len(vals)+1)
    plt.figure(figsize=(8,3.5))
    plt.plot(xs, vals)
    plt.xlabel("反復回数 (iteration)")
    plt.ylabel(metric_key.upper())
    best_it = getattr(clf, "best_iteration_", "NA")
    plt.title(f"検証 {metric_key.upper()} の推移（best_iter={best_it}）")
    savefig("learning_curve.png")
    plt.tight_layout()
    plt.show()


# ========================
# 7) テキスト出力（表＆要約）— 日本語
# ========================
def metrics_from_cm(cm):
    tn, fp, fn, tp = cm.ravel()
    acc = (tp+tn)/(tp+tn+fp+fn)
    prec = tp/(tp+fp) if (tp+fp)>0 else 0.0
    rec  = tp/(tp+fn) if (tp+fn)>0 else 0.0
    spec = tn/(tn+fp) if (tn+fp)>0 else 0.0
    return acc, prec, rec, spec


acc05, prec05, rec05, spec05 = metrics_from_cm(cm_05)
accB,  precB,  recB,  specB  = metrics_from_cm(cm_best)

summary = pd.DataFrame({
    "指標": [
        "ROC-AUC", "PR-AUC(AP)", "Brier",
        "F1@0.50", "Accuracy@0.50", "Precision@0.50", "Recall@0.50", "Specificity@0.50",
        "F1@最良閾値", "最良閾値",
        "Accuracy@最良", "Precision@最良", "Recall@最良", "Specificity@最良",
        "best_iteration"
    ],
    "値": [
        auc, ap, brier,
        f1_05, acc05, prec05, rec05, spec05,
        f1_best, best_th,
        accB,  precB,  recB,  specB,
        getattr(clf, "best_iteration_", np.nan)
    ]
})

print("\n=== 評価サマリー ===")
print(summary.to_string(index=False))

print("\n=== 分類レポート（閾値=0.50）===")
# ラベルの順を [0,1] に固定し、日本語クラス名を指定
print(classification_report(y_te, pred_05, labels=[0,1],
                            target_names=[CLASS_LABELS[0], CLASS_LABELS[1]]))

print(f"\n=== 自動要約 ===\n"
      f"- ROC-AUC: {auc:.4f} / PR-AUC(AP): {ap:.4f} / Brier: {brier:.4f}\n"
      f"- 0.50閾値のF1: {f1_05:.4f}（Accuracy={acc05:.4f}, Precision={prec05:.4f}, Recall={rec05:.4f}）\n"
      f"- 最良閾値: {best_th:.2f} → F1={f1_best:.4f}（混同行列は『cm_best』参照）\n"
      f"- 重要度上位（日本語）は『feature_importance_split_top15.png』に保存\n"
      f"- すべての図は ./{OUT_DIR}/ に保存済み\n")

まずはこの「早期停止＋AUC」をベースに、num_leaves と learning_rate×n_estimators を調整するのが近道です。

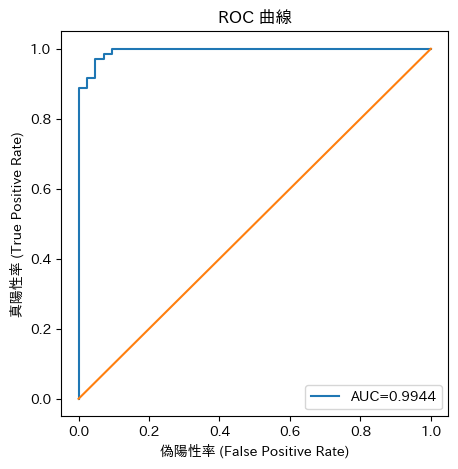
ROC曲線

ROC曲線

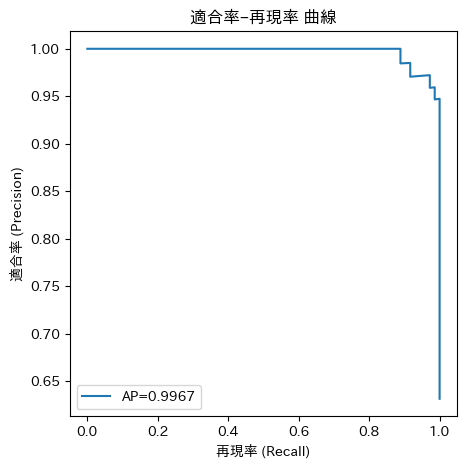
Precision-Recall曲線

Precision-Recall曲線

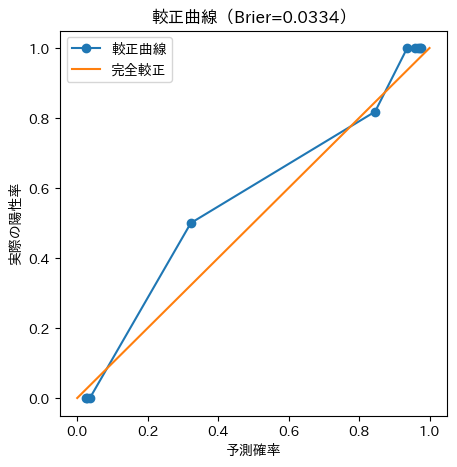
キャリブレーション曲線

キャリブレーション曲線

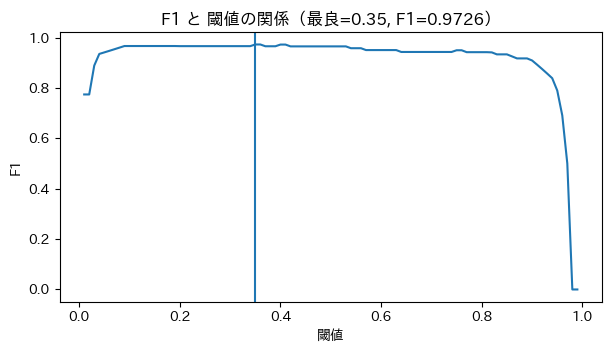
閾値vs F1スコア

閾値vs F1スコア

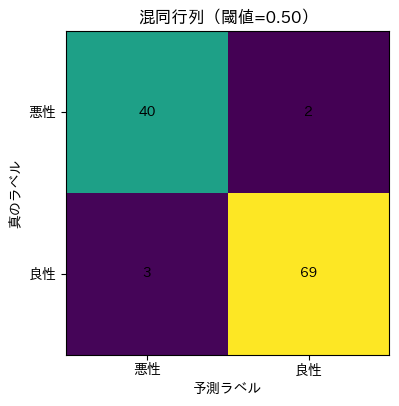
混同行列（閾値0.50）

混同行列（閾値0.50）

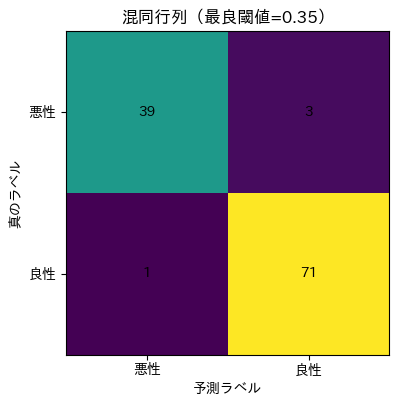
混同行列（最良閾値）

混同行列（最良閾値）

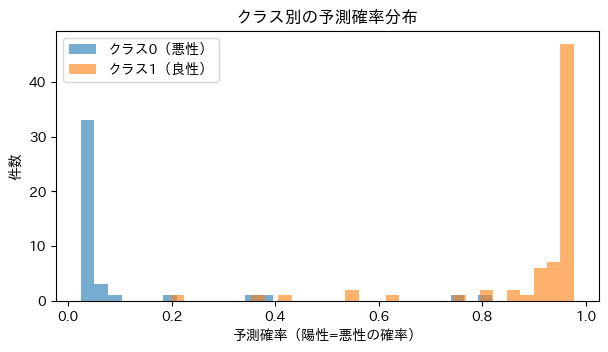
クラス別確率分布

クラス別確率分布

よく使うハイパーパラメーター（まずはここだけ）

  • 表現力と過学習
    • num_leaves：葉数。大きいほど表現力↑だが過学習↑。
    • max_depth：深さ上限。Leaf-wise の暴走を抑えるガード。
    • min_data_in_leaf（=min_child_samples）：葉に必要な最少サンプル数（過学習抑制）。
  • 学習率・木の本数
    • learning_rate を下げ、n_estimators を増やし、早期停止で実質回数を調整。
  • サブサンプリング
    • subsample（行） / colsample_bytree（列）：汎化↑・速度↑。
  • 正則化
    • lambda_l1, lambda_l2, min_gain_to_split。
  • 不均衡（分類）
    • class_weight="balanced" または scale_pos_weight。
  • 目的関数（例）
    • 回帰：l2 / l1 / huber / poisson（カウント）
    • 分類：binary / multiclass
    • ランキング：lambdarank
    • 区間予測：quantile（alpha で分位点を指定）

カテゴリ＆欠損の扱い（前処理ほぼ不要）

  • カテゴリ：文字列→整数化して渡す。pandas なら astype("category").cat.codes が簡単。
    scikit-learn API では categorical_feature に**列名（または番号）**を渡すのが確実。

    python
    cat_cols = ["prefecture", "weekday"]
for c in cat_cols:
    X[c] = X[c].astype("category").cat.codes
clf.fit(X_tr, y_tr, categorical_feature=cat_cols, ...)

    ※ 学習時に存在しないカテゴリが推論時に出ると 未定義 になるため、エンコードの辞書を保存して再利用するのが安全。

  • 欠損：NaN のままで OK。LightGBM が分割時に既定方向を自動学習します。意味のある欠損（たとえば「センサー断」で 0 が入る等）は欠損フラグ列を追加すると効くことがあります。

ありがちミスと対策

  • （回帰）高い値を恒常的に下振れ
    → 損失の性質。objective="poisson"、huber、ターゲットを log1p 変換して学習（推論で expm1 で戻す）を試す。

  • Leaf-wise で過学習
    → num_leaves を小さめに、max_depth を設定、min_data_in_leaf を増やす、サブサンプリングと L1/L2 を加える。

  • カテゴリ列を文字列のまま投入
    → 整数化して categorical_feature を指定。前処理の一貫性（学習時と推論時）に注意。

  • 評価リーク（時系列）
    → 「過去→未来」の分割（TimeSeriesSplit）に変更。ラグ/移動平均は未来を見ないよう注意。

XGBoost / CatBoost との違い（要点）

  • 木の成長：XGBoost は基本 深さ優先（level-wise）、LightGBM は 葉優先（leaf-wise）。同じ葉数なら LightGBM は損失を下げやすいが過学習に注意。
  • 分割探索：両者ともヒストグラム法を持つが、LightGBM は当初からヒストグラム最適化に特化し、GOSS/EFB と組み合わせて高速化。
  • カテゴリ処理：CatBoost はターゲット統計を用いた独自のカテゴリ処理が強み。LightGBM は整数カテゴリ＋最適2分割で実務十分な精度と速度のバランス。

より実務寄りのチューニング手順

  1. ベースライン：主要カテゴリ・ラグ（時系列なら）・早期停止つきでまず学習。
  2. 表現力：num_leaves→max_depth→min_data_in_leaf の順で過学習しない最大点を探る。
  3. 汎化 & 速度：subsample / colsample_bytree、必要なら max_bin を下げる。
  4. 目的関数：誤差の性質（外れ値／カウント／ピーク重視）に合わせて l2/l1/huber/poisson/quantile を切り替え。
  5. ビジネス指標に合わせた評価：AUC/PR-AUC（分類）、MAE/RMSE（回帰）に加え、上位デシル誤差やコスト重みを確認。
  6. 安定化：交差検証（IID）または時系列CVで再現性を確認し、学習曲線や残差のドリフトも可視化。

参考文献